Breaking by bending

The coolest thing about slender objects is that they can undergo large shape changes at very little energy cost (and hence only small stresses and strains). As illustration, bending a plate of thickness $t$ into a cylinder of radius $R$ incurs strains only $\sim t/R \ll 1$. So slender mechanics involves lots of shapes and geometry, which is always nice. However, a second cool thing about slender objects occurred to me just now while using my teeth to shred the stick from my 2nd Magnum of the evening: they allow us to generate large stresses very easily. In spirit, this second cool thing almost pushes against the first!

Take my Magnum stick as an example (or a twig if you prefer). It’s basically a rod of thickness $t$ (made of fibrous material with the fibres aligned with its long direction). Toying with it, it’s pretty clear that to break it by pulling along its length would be extremely hard. Even if I had a pair of pliers in each hand that could grip the rod really well, I don’t think I could do it. This tells us that the force $f$ I can pull with, divided by the cross-sectional area $\sim t^2$ of the rod, is smaller than the stress required to break the rod’s fibres and fracture the material. On the other hand, snapping the rod by bending it is trivially easy, e.g. by pulling down with an index finger at each end while a thumb in the middle pushes up (fig. 1). So somehow applying a bending deformation instead of an axial deformation allows us to generate stresses $\gg f/t^2$.

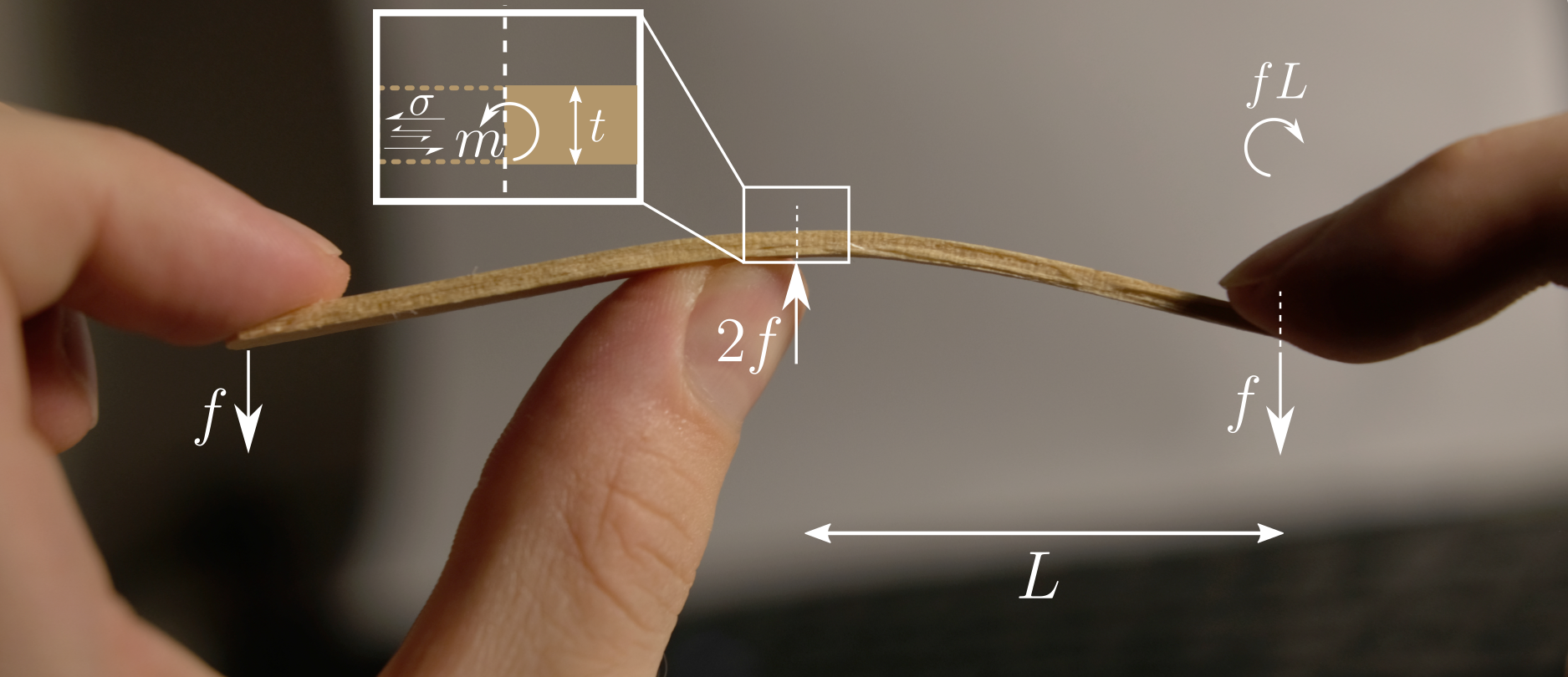
Fig. 1: The left-hand half of the rod exerts stress $\sigma$ on the right-hand half, non-uniform over the cross-section. The resulting bending moment $m \sim \sigma t^3$, as it must by dimensional analysis.

How does this work? Well, suppose the rod’s length is $2L$, and consider moment equilibrium of the half of the rod to the right of my thumb, taking moments about the rod’s midpoint. For equilibrium, the left half of the rod must exert (on the right half) a moment $m = f L$ anticlockwise at the midpoint, to balance the moment of $f L$ clockwise exerted by my right index finger. But the left half can only exert such a moment by exerting a tensile stress that is non-uniform through the thickness. In scaling terms the resulting moment $m \sim \sigma t^3$ where $\sigma$ is the scale of the non-uniform stress. Thus moment equilibrium requires $\sigma \sim f L / t^3$, much larger than the stress $\sim f / t^2$ we can generate by pulling axially. So, at the rod’s midpoint at least, the stress is amplified in the bending deformation as opposed to the pure stretching deformation. Leverage, of a kind :)