Complex numbers and vectors

I’ve been thinking a bit about complex numbers and why we use them. Complex numbers are just arrows in the 2D plane. They are thus essentially just 2D vectors in the 2D Euclidean plane, with some extra rules operations on them defined on top of the usual ones (addition, dot product etc), which turn out to be very useful. The fact that these extra operations sometimes involve rotations means that complex numbers provide a convenient way of representing 2D rotations (and hence oscillations/sinusoids etc, which are projections of rotations). Quaternions with zero real part have the same kind of relationship to 3D rotations, hence their common use in graphics and similar.

This means that any time we write complex numbers down, we’re really working with some 2D vectors with some fancy operations. This means we should be able to translate between the two languages if we think a bit, because they are really doing the same kind of thing! We’ll use the symbol $\sim$ to represent correspondence/translation between the two representations.

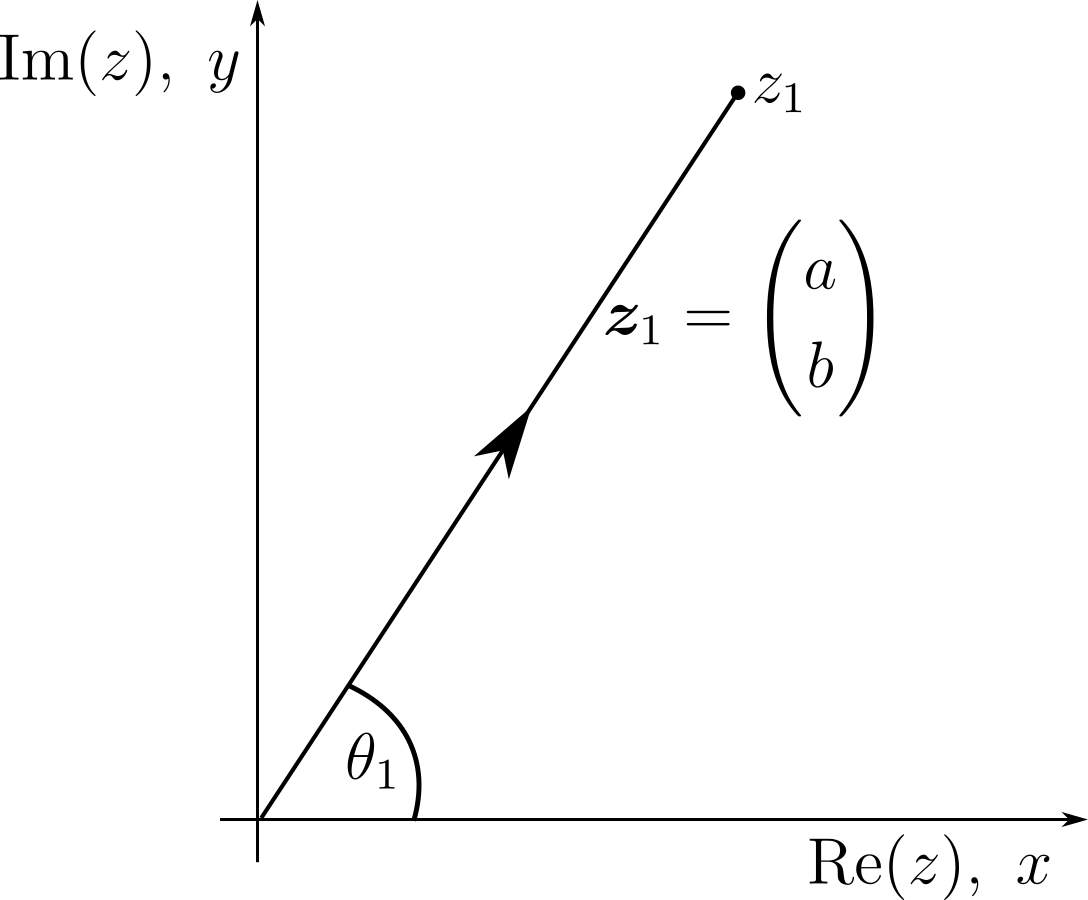
A complex number $z_1$, and its corresponding vector $\mathbf{z}_1$. We write their correspondence as $z_1 \sim \mathbf{z}_1$.

Let’s define two complex numbers $z_1 = a + bi$ and $z_2 = c+di$, and two 2D vectors that correspond to these $\mathbf{z}_1 = a \mathbf{\hat{x}} + b \mathbf{\hat{y}}$ and $\mathbf{z}_2 = c \mathbf{\hat{x}} + d \mathbf{\hat{y}}$. The complex conjugate operation is as usual defined as $z_1^* \equiv a - bi$, which we immediately see is equivalent to a reflection through the $x$-axis, i.e. $$z^* \sim \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \mathbf{z} .$$

Now, $z_1 + z_2 \sim \mathbf{z}_1 + \mathbf{z}_2$ is fairly immediate. Then it’s straightforward to check that $\mathbf{z}_1 \cdot \mathbf{z}_2 = ac + bd = (z_1^* z_2 + z_1 z_2^*)/2$. And this then makes it straightforward to check that $|z_1 + z_2| \equiv \sqrt{(z_1+z_2)(z_1^*+z_2^*)} = |\mathbf{z}_1+\mathbf{z}_2|$ as it had better be!

What about $z_1 z_2$ in vector language? Let’s define $\theta_1 \equiv \mathrm{arg}(z_1)$. Then, a good exercise is to use the form $z = |z| e^{i\theta}$ to (slightly tediously) prove $z_1 z_2 = ac-bd +(bc + ad)i$ (hint: use $e^{i\theta} = \cos(\theta) + i\sin(\theta)$ and some basic trig identities). While doing that, you’ll find $$\begin{aligned} z_1 z_2 = |z_1||z_2| &\bigg[\cos(\theta_1)\cos(\theta_2) - \sin(\theta_1)\sin(\theta_2)\\ &+ \left(\sin(\theta_1)\cos(\theta_2) + \cos(\theta_1)\sin(\theta_2) \right) i \bigg] , \end{aligned}$$ and thus, translating to vector form, $$\begin{aligned} z_1 z_2 \sim |z_1||z_2| &\bigg[\left( \cos(\theta_1)\cos(\theta_2) - \sin(\theta_1)\sin(\theta_2) \right) \mathbf{\hat{x}} \\ &+ \left(\sin(\theta_1)\cos(\theta_2) + \cos(\theta_1)\sin(\theta_2) \right) \mathbf{\hat{y}} \bigg] . \end{aligned}$$ We can write this fully vectorially as $$\begin{aligned} z_1 z_2 \sim &\left( (\mathbf{z}_1 \cdot \mathbf{\hat{x}}) (\mathbf{z}_2 \cdot \mathbf{\hat{x}}) - (\mathbf{z}_1 \cdot \mathbf{\hat{y}})(\mathbf{z}_2 \cdot \mathbf{\hat{y}}) \right) \mathbf{\hat{x}} \\ &+ \left((\mathbf{z}_1 \cdot \mathbf{\hat{y}})(\mathbf{z}_2 \cdot \mathbf{\hat{x}}) + (\mathbf{z}_1 \cdot \mathbf{\hat{x}})(\mathbf{z}_2 \cdot \mathbf{\hat{y}}) \right) \mathbf{\hat{y}} , \end{aligned}\label{eq:z1z2_mess}\tag{1}$$ but that’s really not very illuminating. But we can also write it as $$z_1 z_2 \sim |z_1||z_2| \bigg[\cos(\theta_1+\theta_2) \mathbf{\hat{x}} + \sin(\theta_1+\theta_2)\mathbf{\hat{y}} \bigg] , \label{eq:z1z2_usual}\tag{2}$$ which makes manifest the usual picture for multiplying complex numbers: the new magnitude is the product of the old two, and the new argument is the sum of the old two. The operation on the argument is clearly a particular rotation in the 2D plane, so we should search for a form that makes that explicit! We can do that just by factorising eq. \ref{eq:z1z2_mess} to find $$z_1 z_2 \sim \begin{pmatrix} \mathbf{z}_2 \cdot \mathbf{\hat{x}} & -\mathbf{z}_2 \cdot \mathbf{\hat{y}} \\ \mathbf{z}_2 \cdot \mathbf{\hat{y}} & ~~\mathbf{z}_2 \cdot \mathbf{\hat{x}} \end{pmatrix} \mathbf{z}_1 = \begin{pmatrix} \cos \theta_2 & -\sin \theta_2 \\ \sin \theta_2 & ~~\cos \theta_2 \end{pmatrix} |\mathbf{z}_2| \, \mathbf{z}_1 \label{eq:z1z2_matrix}\tag{3}$$ where the matrix is an anticlockwise rotation by $\theta_2$ combined with a multiplication by $|\mathbf{z}_2|$, again fitting with the usual picture. Note that this rotation really does care which directions in the 2D plane are your $\mathbf{\hat{x}}$ and $\mathbf{\hat{y}}$ directions, which is partly why the complex number representation is nice - it hides this ugliness!

What about the ‘2D cross product’, $\overset{\scriptscriptstyle{\mathrm{2D}}}{\times}$, of $\mathbf{z}_1$ and $\mathbf{z}_2$? By that I mean $$\mathbf{z}_1 \overset{\scriptscriptstyle{\mathrm{2D}}}{\times} \mathbf{z}_2 = \left( \mathbf{z}_1 \cdot \mathbf{\hat{x}} \right) \left( \mathbf{z}_2\cdot \mathbf{\hat{y}} \right) - \left( \mathbf{z}_1 \cdot \mathbf{\hat{y}} \right) \left( \mathbf{z}_2\cdot \mathbf{\hat{x}} \right) = \varepsilon^{jk} z_1^j z_2^k \label{eq:2dcross}\tag{4}$$ where $$\varepsilon^{12} = -\varepsilon^{21} = 1, ~~~~~ \varepsilon^{11} = \varepsilon^{22} = 0,$$ and we’ve used the Einstein summation convention. This is equivalent to thinking of $\mathbf{z}_1$ and $\mathbf{z}_2$ as 3D vectors, taking their usual 3D cross product and then extracting just the $z$-component. From the middle expression in eq. \ref{eq:2dcross} we quickly find $$\mathbf{z}_1 \overset{\scriptscriptstyle{\mathrm{2D}}}{\times} \mathbf{z}_2 = |z_1||z_2| \sin(\theta_2 - \theta_1),$$ as is familiar from the 3D cross product. Note the above expression equals the area of the parallelogram with $\mathbf{z}_1$ and $\mathbf{z}_2$ as sides. From the final expression in eq. \ref{eq:2dcross} we quickly find something that’s in a way nicer: $$\mathbf{z}_1 \overset{\scriptscriptstyle{\mathrm{2D}}}{\times} \mathbf{z}_2 = ad - bc = \frac{i}{2} \left(z_1z_2^* - z_1^* z_2 \right).$$

So overall I’d say that the dot and cross product expressions are a tad more complicated translated into complex numbers and their conjugates. But $z_1 z_2$ is far, far nicer than the corresponding bulky vectorial expressions shown in eqs \ref{eq:z1z2_usual} and \ref{eq:z1z2_matrix}. Thus, for finding things like dot and cross products, complex numbers aren’t particularly slick or helpful, but if you want to keep track of *phase* (i.e. angle relative to the $x$-axis) that is changing or calculated from some combination of quantities with their own phases, complex numbers provide an extremely elegant and compact way to do this via multiplication. We can summarise our results as follows, where the matrix multiplications are applied to $x$- and $y$-components: $$\begin{array}{ |c|c|c| } \hline \text{Complex numbers} & \text{Relationship} & \text{Vectors} \\ \hline z = a+bi = |z|e^{i\theta} & \sim & \mathbf{z} = a \mathbf{\hat{x}} + b\mathbf{\hat{y}} \\ z^* & \sim & \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \mathbf{z} \\ z_1 + z_2 & \sim & \mathbf{z}_1 + \mathbf{z}_2 \\ (z_1^* z_2 + z_1 z_2^*)/2 & = & \mathbf{z}_1 \cdot \mathbf{z}_2 \\ |z_1 + z_2| & = & |\mathbf{z}_1 + \mathbf{z}_2| \\ z_1 z_2 & \sim & \begin{pmatrix} \cos \theta_2 & -\sin \theta_2 \\ \sin \theta_2 & ~~\cos \theta_2 \end{pmatrix} |\mathbf{z}_2| \, \mathbf{z}_1 \\ i \left(z_1z_2^* - z_1^* z_2 \right)/2 & = & \mathbf{z}_1 \overset{\scriptscriptstyle{\mathrm{2D}}}{\times} \mathbf{z}_2 \\ \hline \end{array} \notag$$