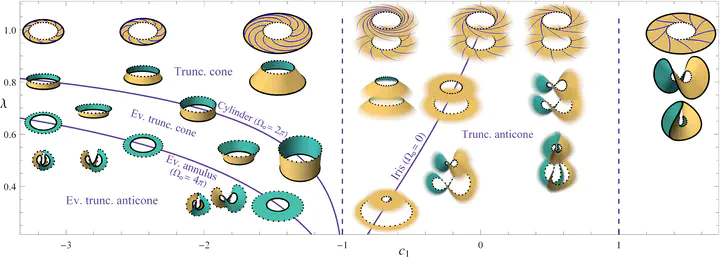
Abstract
Liquid crystal elastomers contract along their director on heating and recover on cooling, offering great potential as actuators and artificial muscles. If a flat sheet is programmed with a spatially varying director pattern, it will actuate into a curved surface, allowing the material to act as a strong machine such as a grabber or lifter. Here we study the actuation of programmed annular sheets which, owing to their central hole, can sidestep constraints on area and orientation. We systematically catalogue the set of developable surfaces encodable via axisymmetric director patterns, and uncover several qualitatively new modes of actuation, including cylinders, irises, and everted surfaces in which the inner boundary becomes the outer boundary after actuation. We confirm our designs with a combination of experiments and numerics. Many of our actuators can re-attain their initial inner or outer radius upon completing actuation, making them particularly promising, as they can avoid potentially problematic stresses in their activated state even when fixed onto a frame or pipe.